Lei de Amdahl
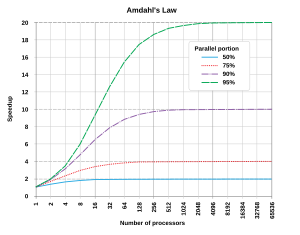
A lei de Amdahl, também conhecida como argumento de Amdahl,[1] é usada para encontrar a máxima melhora esperada para um sistema em geral quando apenas uma única parte dele é melhorada. Isto é frequentemente usado em computação paralela para prever o máximo speedup teórico usando múltiplos processadores. A lei possui o nome do Arquiteto computacional Gene Amdahl, e foi apresentada a AFIPS na Conferência Conjunta de Informática na primavera de 1967.
O speedup de um programa usando múltiplos processadores em computação paralela é limitado pelo tempo necessário para a fração sequencial de um programa. Por exemplo, se o programa precisa de 20 horas usando um único núcleo de processamento, e a parte específica de um programa que demora uma hora para executar não pode ser paralelizado, enquanto as 19 horas restantes (95%) do tempo da execução pode ser paralelizado, independente de quantos processadores são dedicados a execução paralela deste programa, o tempo de execução mínima não pode ser menor que aquela crítica uma hora. Por isso o aumento de velocidade é limitado em no máximo 20x.
Speedup
Speedup pode ser definido como a relação entre o tempo gasto para executar uma tarefa com um único processador e o tempo gasto com N processadores, ou seja, Speedup é a Medida do ganho em tempo.
Onde 'S' é o speedup e 'T'(N) é o tempo gasto para 'N' processadores
Definição
Fórmulas:
- , o número de threads de execução,
- , fração de um algoritmo estritamente serial,
O tempo que um algoritmo demora para terminar a execução utilizando thread(s) de execução, corresponde a:
Portanto,o speedup teórico que pode ser obtido pela execução de um dado algoritmo, em um sistema capaz da execução de threads de execução, é:
Descrição
A Lei de Amdahl é um modelo de "speedup esperado" sobre a relação entre implementação paralelizada de um algoritmo e sua implementação sequencial, sob a suposição de que o tamanho do problema continua a ser o mesmo quando paralelizado. Por exemplo, se para um determinado problema de execução em paralelo de um algoritmo, pode ser executado apenas 12% das operações do algoritmo deste modo (enquanto os restantes 88% das operações não são paralelizável), a Lei de Amdahl afirma que o speedup máximo da versão paralelizada é 1/(1 – 0.12) = 1.136 vezes mais rápido que uma versão não paralelizada.
Mais tecnicamente, a lei se dedica ao aumento do speedup realizável com um melhoramento do cálculo que afeta a proporção "P" de um cálculo onde o melhoramento tem um speedup de “S”. (Por exemplo, se 30% do cálculo pode ser objeto de um melhoramento da velocidade, “P" será 0.3, se o melhoramento fizer a porção afetada duas vezes mais rápida, “S" será 2). A Lei de Amdahl afirma que o aumento do speedup aplicando o melhoramento será:
Para ver como essa fórmula foi derivada, assume-se que o tempo de execução do antigo cálculo era 1, por alguma unidade de tempo. O tempo de funcionamento do novo cálculo será a duração da fração não melhorada (que é 1 − ‘’P"), mais a duração da fração de tempo melhorada. O período de tempo para a parte melhorada do cálculo é a duração do tempo de execução das partes melhoradas dividida pelo speedup, ou seja “P”/“S". O speedup final é calculado pela divisão do antigo tempo de duração pelo novo tempo de duração, que é a função da fórmula acima.
Aqui, outro exemplo, nos é dado uma tarefa sequencial que é dividido em quatro partes consecutivas: P1, P2, P3 e P4 com as porcentagens de tempo de execução começando em 11%, 18%, 23% e 48% respectivamente. Em seguida, houve a informação que P1 não é acelerado, então S1 = 1, enquanto P2 é acelerado 5x, P3 é acelerado 20x, e P4 é acelerado 1.6x. Utilizando a fórmula P1/S1 + P2/S2 + P3/S3 + P4/S4, então encontra-se uma nova execução sequencial, que é:
ou um pouco menos que 1⁄2 do tempo de execução original. Usando a fórmula (P1/S1 + P2/S2 + P3/S3 + P4/S4)−1, o aumento de velocidade geral é 1 / 0.4575 = 2.186, ou seja, um pouco mais que o dobro da velocidade original. Note como o aumento de 20x e 5x não possui muito efeito sobre a velocidade total quando P1 (11%) não é acelerado, e P4 (48%) é acelerado apenas 1.6 vezes.
Paralelização
No caso da paralelização, a lei de Amdahl afirma que ‘'P" é a proporção de um programa que pode ser feito paralelamente (i.e, benefício da paralelização), e (1 - P) é a proporção que não pode ser paralelizada (permanece serial), o speedup máximo que pode ser atingido usando ‘'N" processadores é
- .
No limite, como ‘'N" tende ao infinito, o speedup máximo tende ser 1 / (1 - ‘’P’). Na prática, o desempenho à relação preço cai rapidamente como N é aumentada uma vez que há mesmo um pequeno componente de (1 - P).
Como exemplo, se “P" é 90%, então (1 - “P”) é 10%, e o problema pode ser acelerado por um fator máximo de 10, não interessa o quão grande o valor usado para “N”. Por essa razão, computação paralela é apenas útil para qualquer pequeno número de processadores, ou problemas com valores muito grandes de “P”: chamado "problemas embaraçosamente paralelos". Uma grande parte do ofício de programação paralela consiste em tentar reduzir o componente (1 - P) para o menor valor possível.
"P" pode ser estimada por meio do aumento de velocidade (SU) sobre um número específico de processadores (NP) usando:
- .
P estimado desta forma pode então ser utilizado na Lei de Amdahl para prever o aumento de velocidade para um número diferente de processadores.
Relação à lei dos rendimentos decrescentes
A lei de Amdahl é muitas vezes confundida com a lei dos rendimentos decrescentes, enquanto apenas um caso especial da aplicação da Lei de Amdahl se comporta como esta. Se alguém pega ótimamente (em termos de speed-up alcançado) o que melhorar, então verá melhorias monotonicamente decrescentes. Se, no entanto, pega algo não-ideal, depois de melhorar um componente sub-ótimo e seguir em frente para melhorar o componente não-ideal, pode-se ver um aumento no retorno. Note-se que muitas vezes é racional para melhorar um sistema numa ordem que é "não-ótima", melhorias que são mais difíceis, ou que consomem mais tempo de desenvolvimento do que os outros.
Lei de Amdahl representa a "lei de rendimentos decrescentes" se você está considerando qual ordem de retorno que você obterá adicionando mais processadores a uma máquina, se você estiver realizando uma executação em computação de tamanho fixo que vai usar todos os processadores disponíveis para a sua capacidade. Cada novo processador que você adicionar ao sistema irá aumentar menos o poder de execução do que o anterior. Cada vez que você dobrar o número de processadores a relação de aumento de velocidade vai diminuir, como a taxa de transferência total para o limite de .
Esta análise negligencia outros gargalos potenciais, tais como banda de memória e largura de banda de I/O, se eles não se ajustarem junto ao número de processadores; no entanto, tendo em conta esses gargalos tenderia a demonstrar ainda mais os retornos decrescentes por acrescentar apenas processadores.
Speedup em um programa sequencial
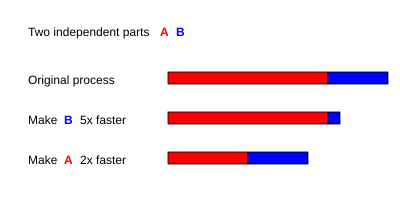
O speedup máximo de um programa sequencial melhorado, onde uma parte foi acelerada vezes, é limitada pela irregularidade.
onde () é a fração de tempo (antes do melhoramento) gasto na parte que não foi melhorada. Por exemplo (veja a figura ao lado direito):
- Se a parte B é executada cinco vezes mais rápida (), , , e , então
- Se a parte A é executada duas vezes mais rápida (), , , e , então
Portanto, tornando A duas vezes mais rápido é melhor que tornar B cinco vezes mais rápido. A porcentagem de melhoria da velocidade pode ser calculada como:
- Melhorando a parte A por um factor de dois irá aumentar a velocidade global do programa por um factor de 1,6, o que faz com que seja 37,5% mais rápido do que o cálculo inicial.
- No entanto, a melhoria da parte B por um fator de cinco, que, presumivelmente, exige mais esforço, só irá atingir um fator de aceleração geral de 1,25, o que o torna 20% mais rápido.
Limitações
A lei de Amdahl só se aplica aos casos em que o tamanho do problema está corrigido. Na prática, como mais recursos de computação se tornam disponíveis, eles tendem a se acostumar com problemas maiores (maiores conjuntos de dados), e o tempo gasto na parte paralelizável geralmente cresce muito mais rápido do que o trabalho inerentemente seqüencial. Neste caso, lei de Gustafson dá uma avaliação mais realista do desempenho paralelo.[2]
Notas
- ↑ (Rodgers 1985, p. 226)
- ↑ Michael McCool; James Reinders; Arch Robison (2013). Structured Parallel Programming: Patterns for Efficient Computation. [S.l.]: Elsevier. 61 páginas
Ver também
Referências
- Rodgers, David P. (Junho de 1985). «Improvements in multiprocessor system design». New York, NY, USA: ACM. ACM SIGARCH Computer Architecture News archive. 13 (3): 225–231. ISBN 0-8186-0634-7. ISSN 0163-5964. doi:10.1145/327070.327215
Leitura complementar
- Amdahl, Gene M. (1967). «Validity of the Single Processor Approach to Achieving Large-Scale Computing Capabilities» (PDF). AFIPS Conference Proceedings (30): 483–485. doi:10.1145/1465482.1465560
Ligações externas
- Cases where Amdahl's law is inapplicable
- Oral history interview with Gene M. Amdahl Charles Babbage Institute, University of Minnesota. Amdahl debateu seu trabalho de graduação na Universidade Wisconsin e seu projeto na WISC. Discutiu seu papel na concepção de vários computadores para a IBM, incluindo o STRETCH, IBM 701, e o IBM 704. Ele discutiu seu trabalho com Nathaniel Rochester e com o gerente de processos de design da IBM. Menções do trabalho com Ramo-Wooldridge, Aeronutronic, e a Computer Sciences Corporation
- A simple interactive Amdahl's Law calculator
- "Amdahl's Law" por Joel F. Klein, Wolfram Demonstrations Project, 2007.
- Amdahl's Law in the Multicore Era
- Blog Post: "What the $#@! is Parallelism, Anyhow?"
- Amdahl's Law applied to OS system calls on multicore CPU
- Evaluation of the Intel Core i7 Turbo Boost feature, por James Charles, Preet Jassi, Ananth Narayan S, Abbas Sadat e Alexandra Fedorova
- Calculation of the acceleration of parallel programs as a function of the number of threads, por George Popov, Valeri Mladenov e Nikos Mastorakis











![{\displaystyle B\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65c0053f22ccbf29da660166e9d8a401cb0bcc27)























