Algoritmo de Edmonds-Karp

As referências deste artigo necessitam de formatação. Por favor, utilize fontes apropriadas contendo título, autor e data para que o verbete permaneça verificável. (Janeiro de 2014)

Na Ciência da computação e teoria dos grafos, o Algoritmo de Edmonds-Karp é uma implementação do Algoritmo de Ford-Fulkerson para a resolução do problema de fluxo máximo em uma rede de fluxo. A característica que o distingue é que o caminho de aumento mais curto é usado em cada iteração, o que garante que o calculo vai terminar. Na maioria das implementações, o caminho de aumento mais curto é encontrado usando uma busca em largura, a qual roda em um tempo de ${\displaystyle O(VE^{2})}$. Isto é assintoticamente mais lento que algoritmo remarcagem-para-frente, o qual roda em ${\displaystyle O(V^{3})}$, mas é freqüentemente mais rápido para utilização em grafos esparsos. O algoritmo foi publicado pela primeira vez pelo cientista russo Dinic, em 1970, e depois, de forma independente, por Edmonds e Karp que o publicaram em 1972. O algoritmo de Dinic inclui técnicas adicionais para reduzir o tempo para a ordem de ${\displaystyle O(V^{2}E)}$.

Este algoritmo é idêntico ao Algoritmo de Ford-Fulkerson, exceto que a ordem de busca quando encontra que o caminho de aumento de fluxo definido. O caminho encontrado deve ser o caminho mais curto com capacidade disponível.

Implementação Python:

def edmonds_karp(C, source, sink):
    n = len(C) # C is the capacity matrix
    F = [[0] * n for _ in xrange(n)]
    # residual capacity from u to v is C[u][v] - F[u][v]

    while True:
        path = bfs(C, F, source, sink)
        if not path:
            break
        # traverse path to find smallest capacity
        u,v = path[0], path[1]
        flow = C[u][v] - F[u][v]
        for i in xrange(len(path) - 2):
            u,v = path[i+1], path[i+2]
            flow = min(flow, C[u][v] - F[u][v])
        # traverse path to update flow
        for i in range(len(path) - 1):
            u,v = path[i], path[i+1]
            F[u][v] += flow
            F[v][u] -= flow
    return sum([F[source][i] for i in xrange(n)])

def bfs(C, F, source, sink):
    P = [-1] * len(C) # parent in search tree
    P[source] = source
    queue = [source]
    while queue:
        u = queue.pop(0)
        for v in xrange(len(C)):
            if C[u][v] - F[u][v] > 0 and P[v] == -1:
                P[v] = u
                queue.append(v)
                if v == sink:
                    path = []
                    while True:
                        path.insert(0, v)
                        if v == source:
                            break
                        v = P[v]
                    return path
    return None

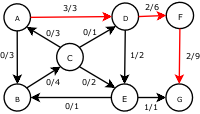
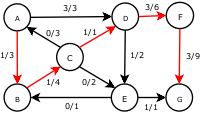
Dada uma rede de sete nós e capacidade como mostrado abaixo:

No pares ${\displaystyle f/c}$ escritos nos arcos, ${\displaystyle f}$ é o fluxo actual, e ${\displaystyle c}$ é a capacidade. A capacidade residual de ${\displaystyle u}$ para ${\displaystyle v}$ é ${\displaystyle c_{f}(u,v)=c(u,v)-f(u,v)}$, a capacidade total, menos a vazão que já esta sendo usada. Se o fluxo da rede de ${\displaystyle u}$ para ${\displaystyle v}$ é negativo, isto contribui para capacidade residual.

Caminho	Capacidade	Rede resultante
${\displaystyle A,D,E,G}$	${\displaystyle \min(c_{f}(A,D),c_{f}(D,E),c_{f}(E,G))=}$ ${\displaystyle \min(3-0,2-0,1-0)=}$ ${\displaystyle \min(3,2,1)=1}$
${\displaystyle A,D,F,G}$	${\displaystyle \min(c_{f}(A,D),c_{f}(D,F),c_{f}(F,G))=}$ ${\displaystyle \min(3-1,6-0,9-0)=}$ ${\displaystyle \min(2,6,9)=2}$
${\displaystyle A,B,C,D,F,G}$	${\displaystyle \min(c_{f}(A,B),c_{f}(B,C),c_{f}(C,D),c_{f}(D,F),c_{f}(F,G))=}$ ${\displaystyle \min(3-0,4-0,1-0,6-2,9-2)=}$ ${\displaystyle \min(3,4,1,4,7)=1}$
${\displaystyle A,B,C,E,D,F,G}$	${\displaystyle \min(c_{f}(A,B),c_{f}(B,C),c_{f}(C,E),c_{f}(E,D),c_{f}(D,F),c_{f}(F,G))=}$ ${\displaystyle \min(3-1,4-1,2-0,0--1,6-3,9-3)=}$ ${\displaystyle \min(2,3,2,1,3,6)=1}$

Note como o comprimento do caminho aumentante encontrado pelo algoritmo nunca diminui. Os caminhos encontrados são os mais curtos possíveis. O fluxo encontrado é igual a capacidade que cruza o menor corte no grafo separando a fonte e o consumo. Há somente um corte mínimo neste grafo, particionando-se os nodos nos conjuntos ${\displaystyle \{A,B,C,E\}}$ e ${\displaystyle \{D,F,G\}}$, com a capacidade ${\displaystyle c(A,D)+c(C,D)+c(E,G)=3+1+1=5}$.

• E. A. Dinic, Algorithm for solution of a problem of maximum flow in a network with power estimation, Soviet Math. Doklady, Vol 11 (1970) pp1277-1280.
• J. Edmonds and R. M. Karp, Theoretical improvements in algorithmic efficiency for network flow problems, Journal of the ACM, Vol 19, No. 2 (1972) pp248-264. PDF (necessita autenticação)